MediaMente: lezione n.1 ("Verso il digitale")

Per capire la rivoluzione in atto nel mondo dei media, e per rendersi conto delle ragioni che hanno reso il computer lo strumento per eccellenza nella gestione di informazione di ogni genere, occorre innanzitutto comprendere un concetto fondamentale: quello di informazione in formato digitale.

Si tratta sicuramente di uno dei concetti-chiave del nostro tempo (non a caso si parla spesso di digital revolution, rivoluzione digitale, e di digital culture, cultura digitale). Eppure molto spesso l'idea che se ne ha è estremamente vaga: l'informazione in formato digitale è quella che può essere manipolata da un computer. Al più - magari ricordando che gli orologi digitali sono quelli nei quali l'ora viene direttamente indicata attraverso numeri anziché attraverso la posizione delle lancette sul quadrante - ci si spinge a collegare il concetto di 'digitale' al termine inglese digit (cifra o numero), compiendo il passo ulteriore di identificare l'informazione in formato digitale con l'informazione in formato numerico.

Ma perché la traduzione dell'informazione in formato numerico è tanto importante? Come avviene questa conversione? E, innanzitutto, cos'è questa informazione che vogliamo convertire in formato digitale?

La risposta a questi interrogativi non richiede affatto, come si potrebbe pensare, competenze tecniche o specialistiche. Al contrario, i concetti di base del mondo del digitale sono assolutamente elementari, alla portata di tutti. E se si vuole capire la portata della rivoluzione che stiamo vivendo, è bene cominciare proprio da qui.

Informazione come scelta

Partiamo dunque dal concetto di informazione. Normalmente, tendiamo ad utilizzare il termine 'informazione' in un senso molto generale: facciamo così, ad esempio, quando parliamo di informazione giornalistica o radiotelevisiva, o quando chiediamo 'una informazione' a qualcuno. Sarebbe difficile definire in maniera rigorosa questo concetto generico di informazione. A ben guardare, vi si confondono diversi significati: l'azione di comunicare una notizia, il contenuto della comunicazione (che a sua volta potrebbe essere distinto nel suo aspetto materiale - ad esempio una successione di caratteri - e nel suo aspetto significativo), le caratteristiche del mezzo di comunicazione usato... E' possibile, tuttavia, provare a definire un concetto specifico di informazione, e vedere poi se, e in che misura, il concetto così definito può essere usato, almeno in alcuni casi, anche per capire di cosa parliamo quando parliamo di informazione in senso più generale.

Consideriamo allora una situazione molto semplice (e probabilmente molto frequente): è estate, fa caldo, stiamo tornando a casa dopo una giornata faticosa, e non vediamo l'ora di infilarci sotto la doccia. Nell'aprire la porta di casa, tuttavia, un dubbio ci assale: siamo sicuri di aver lasciato lo scaldabagno acceso? Nonostante il caldo, la prospettiva di una doccia ghiacciata non ci attrae particolarmente: e se lo scaldabagno è spento, dovremo aspettare almeno un'ora per avere l'acqua a una temperatura accettabile. Ci affrettiamo a controllare: naturalmente, lo scaldabagno è spento. Dovremo deciderci a passare a una caldaia a gas, prima o poi.

Riflettiamo un secondo sulla situazione appena considerata. Nel momento di entrare in casa, ci manca una informazione: l'informazione relativa allo stato dello scaldabagno. Sappiamo che lo scaldabagno può trovarsi in uno fra due stati possibili: acceso, o spento. Ma non sappiamo (è questa l'informazione che ci manca) in quale stato esso si trovi effettivamente.

Una situazione di questo genere ci presenta una scelta fra due alternative (detta spesso scelta binaria). Per controllare lo stato dello scaldabagno, daremo probabilmente un'occhiata alla posizione del suo interruttore: sappiamo infatti che quando l'interruttore è premuto verso l'alto lo scaldabagno è acceso, e quando è premuto verso il basso lo scaldabagno è spento. L'interruttore, oltre ad avere la funzione (se lo premiamo) di cambiare lo stato dello scaldabagno, ha anche la funzione di rappresentare lo stato in cui lo scaldabagno si trova in un determinato momento. Proprio per questo, uno sguardo all'interruttore ci fornisce l'informazione che ci mancava.

Al posto dell'interruttore, potremmo in questo caso usare una lampadina accesa o spenta - potremmo in realtà usare qualunque tipo di rappresentazione che ci metta a disposizione due simboli: uno per lo stato 'acceso', e uno per lo stato 'spento'. Potremmo anche usare dei numeri? Certamente: lo scaldabagno potrebbe ad esempio essere dotato di un piccolo display, una finestrella in cui compare il numero '1' se lo scaldabagno è acceso, e il numero '0' se è spento. Del resto, molti interruttori non portano proprio l'indicazione di un '1' e di uno '0' per rappresentare rispettivamente la posizione 'acceso' e quella 'spento'?

Ebbene, quell''1' e quello '0' sono già una forma di codifica numerica (digitale) di una informazione.

Bella forza, direte voi, questa relativa allo scaldabagno era un'informazione semplicissima, c'erano solo due alternative a disposizione.

Giusto. Prima di prendere in considerazione situazioni più complicate, tuttavia, riflettiamo un momento su questo esempio. Proprio perché semplicissimo, potrà forse aiutarci a capire qualcosa di più sul concetto di informazione.

Innanzitutto, nel caso che abbiamo descritto l'informazione che ci interessava era collegata a una scelta fra più alternative (nel caso specifico, fra due alternative). Non sarà forse possibile estendere questa idea anche ad informazioni di altro tipo?

Ci serve il numero di telefono di un'amica. L'amica abita a Roma, quindi sappiamo che le prime cifre saranno 06. Ma ci mancano le altre. Probabilmente, basandoci sulla normale lunghezza dei numeri telefonici di Roma, ci mancano 7 o 8 cifre. Potremmo provare a comporre, una dopo l'altra, tutte le possibili combinazioni, fino ad arrivare a quella giusta? In teoria sì, in pratica però non lo faremo mai: le combinazioni possibili sono moltissime, provarle tutte sarebbe troppo lungo (e troppo costoso!). Anche in questo caso, l'informazione che ci serve corrisponde alla scelta fra diverse alternative: solo che le alternative possibili sono molte di più.

Supponiamo adesso di considerare un'informazione di tipo un po' diverso: stiamo risolvendo uno schema di parole crociate, e troviamo fra le definizioni "l'autore di Ossi di seppia". Questa volta, dunque, abbiamo a che fare con un nome. Guardando lo schema, vediamo che deve essere lungo sette lettere. C'entra ancora la nostra idea di scelta fra diverse possibili alternative? A ben guardare, sì: in ognuna delle sette caselline dello schema corrispondenti alla nostra definizione dovrà andare una lettera dell'alfabeto. Tutto sta nello scegliere le lettere giuste. Anche qui, dal punto di vista puramente combinatorio le alternative possibili sono numerosissime, da 'Aaaaaaa' a 'Zzzzzzz' (due nomi piuttosto improbabili). E anche qui l'informazione che ci interessa - il nome 'Montale' - corrisponde alla scelta di una fra tali alternative. Se nello schema di parole crociate alcune caselle della definizione che ci interessa (ad esempio la 'M' iniziale e la 'E' finale) sono già riempite, le alternative a nostra disposizione diminuiscono, e diventa più facile individuare la parola cercata.

Sulla base di questi esempi, possiamo dire che, almeno in alcuni casi, tipi diversi di informazione hanno a che fare con un meccanismo di base simile: una situazione di scelta fra più alternative. Più numerose saranno le alternative a nostra disposizione, maggiore sarà il contenuto informativo della nostra scelta.

Ma non sappiamo ancora se, e come, questo meccanismo possa operare nel caso di informazioni che non siano numeriche o testuali - ad esempio nel caso di informazioni visive o sonore. Inoltre, non sappiamo ancora se, e come, una informazione di tipo testuale (ad esempio il nome 'Montale') possa essere trasformata in informazione numerica.

Rappresentazione digitale dell'informazione

L'informazione relativa allo stato dello scaldabagno, abbiamo visto, può essere immediatamente rappresentata in forma numerica: un '1' può indicare lo scaldabagno acceso, uno '0' lo scaldabagno spento. La rappresentazione attraverso '0' e '1' (attraverso cioè un sistema di codifica binaria, che utilizzi due sole cifre) ha un importante vantaggio: i dati binari sono facilmente rappresentabili (e manipolabili) all'interno di un computer. Possiamo così pensare a un computer che, ad esempio, controlli lo stato del nostro scaldabagno, rappresentandolo attraverso una celletta di memoria: la celletta conterrà un '1' se lo scaldabagno è acceso, e uno '0' se è spento.

Incontriamo così uno dei termini-chiave dell'universo digitale, il termine bit.

Un bit, infatti, non è altro che la quantità di informazione fornita dalla scelta fra due alternative diverse, considerate come egualmente probabili.

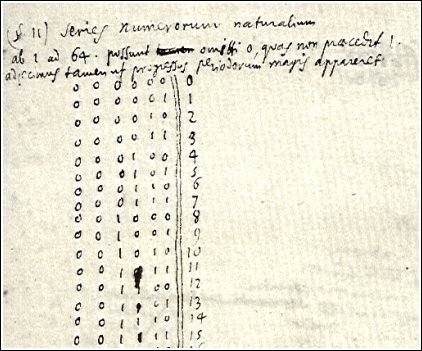
In effetti, l'uso in campo informatico del termine 'digitale' non si riferisce di norma solo al fatto che l'informazione è rappresentata in forma numerica, ma al fatto che è rappresentata in forma numerica sulla base di una codifica binaria, e dunque attraverso bit (il termine bit corrisponde alla contrazione dell'inglese binary digit, numero binario).

Rappresentare in forma binaria una qualsiasi informazione numerica (come il numero di telefono del nostro secondo esempio) è compito relativamente facile. È vero che in genere siamo abituati a utilizzare un sistema di numerazione decimale (i numeri sono costruiti utilizzando le dieci cifre 0,1,2,3,4,5,6,7,8,9). Sappiamo però che ogni numero decimale può essere trasformato in un numero binario (costruito usando solo lo '0' e l''1'). Come? Ebbene, lo '0' e l''1' resteranno uguali, ma il 2 sarà rappresentato dalla combinazione '10', il 3 da '11', il 4 da '100', il 5 da '101', il 6 da '110', il 7 da '111', l'8 da '1000' e così via: la nostra rappresentazione dei numeri superiori a 2 sarà cioè ottenuta combinando fra loro (in maniera ordinata) un numero via via maggiore di '0' e di '1', proprio come nel nostro familiare sistema decimale i numeri superiori al 9 vengono costruiti combinando fra loro (in maniera ordinata) le dieci cifre che abbiamo a disposizione. (si veda la tabella 1).

Una calcolatrice binaria realizzata in Javascript

Inserire un numero da 0 a 65535 nel campo 'decimali' e premere il tasto TAB per ottenere l'equivalente esadecimale. Immettere, invece, un numero da 0 a 255 e premere il tasto TAB, per ottenere anche l'equivalente binario.

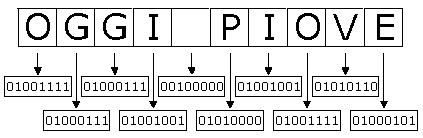
Dai numeri al testo, dal testo ai numeri

Nel caso dei numeri, dunque, non dobbiamo fare altro che passare da una notazione all'altra. Ma come fare per codificare in formato binario una informazione di tipo testuale? Basterà pensare al fatto che un testo non è altro che una successione di caratteri, e che i caratteri di base - quelli compresi nell'alfabeto della lingua usata - sono in un numero che varia col variare delle lingue, ma che è comunque - almeno per le lingue basate sull'alfabeto latino - finito e piuttosto ristretto. Il nostro compito consisterà allora nello stabilire una tabella di corrispondenza fra caratteri da un lato e numeri binari dall'altro. Dovremo ricordarci di includere fra i caratteri da codificare tutti quelli che vogliamo effettivamente differenziare in un testo scritto: se vogliamo poter distinguere fra lettere maiuscole e minuscole dovremo dunque inserirvi l'intero alfabeto sia maiuscolo che minuscolo, se vogliamo poter inserire nei nostri testi anche dei numeri decimali dovremo inserire le dieci cifre (0,1,2,3,4,5,6,7,8,9), se vogliamo poter utilizzare segni di interpunzione (punto, virgola, punto e virgola....) dovremo inserire i caratteri corrispondenti, e così via... senza dimenticare naturalmente di includere lo spazio per separare una parola dall'altra!

Una tabella di questo tipo si chiama tabella di codifica dei caratteri. Per molto tempo, la codifica di riferimento è stata la cosiddetta codifica ASCII (American Standard Code for Information Interchange; attenzione: si scrive ASCII ma si legge con la 'c' dura: 'aski'), riportata nella tabella 2. La codifica ASCII originaria (ASCII stretto) permetteva di distinguere 128 caratteri diversi; la tabella di caratteri attualmente più usata, denominata ISO Latin 1, distingue 256 caratteri, i primi 128 dei quali sono 'ereditati' dall'ASCII stretto. L'indicazione ISO indica l'approvazione da parte dell'International Standardization Organization (si veda al riguardo la scheda di approfondimento), e 'Latin 1' indica che si tratta della tabella di riferimento per gli alfabeti di tipo latino. È questa la codifica di caratteri utilizzata dalla maggior parte dei sistemi operativi (Windows, Macintosh...). Come ogni tabella di codifica dei caratteri, anche la tabella ISO Latin 1 codifica i caratteri da essa previsti (che come si è accennato sono 256) facendo corrispondere a ciascuno un numero binario. Il primo di questi caratteri corrisponderà al numero binario '00000000', il secondo al numero binario '00000001', il terzo al numero binario '00000010', e così via, fino al duecentocinquantaseiesimo, che corrisponderà al numero binario '11111111'. Se contate, vi accorgerete che questi numeri sono tutti espressi attraverso una notazione 'lunga' esattamente otto cifre binarie, ovvero 8 bit. In sostanza, possiamo 'scriverlo' utilizzando otto cellette affiancate, in ciascuna delle quali può esserci uno '0' o un '1' (nel caso considerato, le cellette conterranno tutte degli '1'). Alle tabelle di codifica dei caratteri è dedicata, in questa dispensa, una scheda di approfondimento.

Cosa vuol dire tutto questo? Che le nostre otto cellette potranno essere usate come 'contenitore' per rappresentare - in formato binario - un qualunque carattere della nostra tavola di codifica: dovremo solo ricordarci, se il numero binario che codifica un determinato carattere è più 'corto' di otto cifre, di farlo precedere da tanti '0' quante sono le cellette rimaste vuote. Così, ad esempio, per rappresentare il carattere che abbiamo fatto corrispondere al numero binario '10' riempiremo le nostre cellette in questo modo: '00000010'.

Riassumiamo: 8 bit possono differenziare fra 256 combinazioni diverse, e dunque una 'parola' lunga 8 bit (otto cellette) può rappresentare, attraverso la sua particolare combinazione di '0' e '1', uno qualunque dei 256 caratteri della nostra tavola di codifica.

Il byte è dunque una unità di misura dell'informazione, e indica la quantità di informazione corrispondente alla scelta fra 256 alternative diverse. Se adottiamo come base per la nostra codifica dei testi una tavola comprendente 256 caratteri, ogni carattere del nostro testo richiederà un byte per essere codificato: in altri termini, 'costerà' un byte.

Sullo schermo, ad esempio utilizzando un programma di videoscrittura, l'utente scriverà (e leggerà) la stringa di testo 'oggi piove'; il computer, dal canto suo, lavorerà invece con la rappresentazione binaria di quella stringa. In generale, tutte le volte che utilizzate un computer per visualizzare un testo scritto o per lavorarvi sopra, lo schermo vi presenterà il testo nella familiare forma alfabetica, ma il computer lavorerà in effetti su quel testo in forma binaria: la tavola di conversione lo aiuterà a 'tradurre' i caratteri alfabetici nella relativa codifica binaria, e viceversa.

Le immagini diventano numeri

VC blocco 3 'Digitalizzazione di informazione complessa'

"Benissimo"- direte voi - "con questo trucco, siamo riusciti a rappresentare in formato digitale (a trasformare cioè in lunghe sequenze di '0' e '1', che il computer è in grado di gestire e manipolare) un testo scritto. Ma come la mettiamo con le immagini e i suoni?"

In effetti, in questi casi la situazione sembra del tutto diversa. In fondo, il testo scritto è già costruito combinando fra loro unità discrete (i singoli caratteri) scelte all'interno di un alfabeto abbastanza limitato. Ma immagini e suoni sono fenomeni che sembrano intrinsecamente analogici, nei quali cioè abbiamo a che fare con sfumature continue (di colori, di tonalità, di frequenza...; alla differenza fra analogico e digitale abbiamo dedicato una breve scheda di approfondimento). Se si ha a che fare con un numero finito, prefissato e non troppo grande di entità discrete, la codifica numerica è in fondo facile: basta contare le diverse entità discrete che possono presentarsi, e attribuire a ciascuna un numero che la rappresenti nella codifica. Ma come la mettiamo con le infinite differenze e sfumature di un'immagine o di un suono?

Per capire in che modo il problema sia stato risolto, partiamo da un'osservazione pratica. Abbiamo tutti familiarità con la televisione, che è uno strumento per visualizzare immagini in movimento (per adesso, mettiamo da parte i suoni). Quando guardiamo la televisione, le immagini che vediamo ci appaiono di norma abbastanza facili da interpretare: possiamo identificare forme e strutture, e ad esempio riconoscere il volto di un attore o di un'attrice. Se ci avviciniamo molto allo schermo, tuttavia, noteremo che quella che a una certa distanza ci era apparsa come un'immagine ben definita e continua si 'sgrana' in piccoli puntini luminosi e colorati (i cosiddetti pixel - termine inglese corrispondente alla contrazione di picture elements). L'immagine che vediamo è in realtà il risultato dell'integrazione dei tanti singoli 'segnali' luminosi emessi da ciascuno dei singoli pixel. La griglia di pixel è talmente fitta da darci un'impressione di continuità.

Per digitalizzare un'immagine (vedi scheda "Le tecnologie di digitalizzazione"), il primo passo è proprio quello di 'sovrapporre' all'immagine analogica (ad esempio una fotografia) una griglia fittissima di minuscole cellette. Ogni celletta sarà considerata come un punto dell'immagine, come un pixel. Naturalmente, a parità di immagine, più fitta è la griglia, più piccole saranno le cellette, e migliore sarà l'illusione di un'immagine continua.

In questo modo, abbiamo sostanzialmente 'scomposto' l'immagine in tanti puntini. Ma non abbiamo ancora risolto il problema della nostra codifica digitale. Per farlo, occorre un passo ulteriore: rappresentare i puntini attraverso numeri. Come procedere? L'idea di base è semplice: utilizzare anche qui una tavola di corrispondenza, che però questa volta, anziché far corrispondere numeri a caratteri, faccia corrispondere numeri a colori diversi, o a sfumature diverse di colore.

I primi personal computer con capacità grafiche, all'inizio degli anni '80, utilizzavano griglie molto larghe (i pixel sullo schermo del computer più che a minuscoli puntini corrispondevano a grossi quadrati) e i colori codificati erano molto pochi (solo il bianco e nero, o al più 8 o 16 colori diversi). L'effetto non era un granché (possiamo farcene un'idea guardando le figure 1, 2 e 3), ma i bit utilizzati per rappresentare l'immagine non erano troppo numerosi. Ad esempio, una griglia di 80 colonne per 60 righe (ancora utilizzata in alcuni piccoli videogiochi portatili con schermo a cristalli liquidi) comprende 80x60=4800 pixel, e se ci limitiamo a due colori (bianco e nero) possiamo rappresentare ogni pixel attraverso un solo bit: l''1' potrà rappresentare il nero e lo '0' il bianco. Con 4800 bit avremo dunque codificato un'immagine, anche se solo in bianco e nero, e ben poco definita.

Figura 2 - Uno dei primi giochi grafici per personal computer: Mcity per Sinclair ZX81 (1981). La grafica è appena accennata, i pixel sono grossi quadrati.

Figura 3 - Pochi colori e una grafica ancora spartana, ma i primi passi avanti si vedono: Hobbit, per Commodore 64 (1982). Basta confrontare queste immagini con quelle di un qualunque videogioco dei nostri giorni per rendersi conto dei progressi fatti - e dell'enorme aumento del 'peso' in bit della grafica utilizzata.

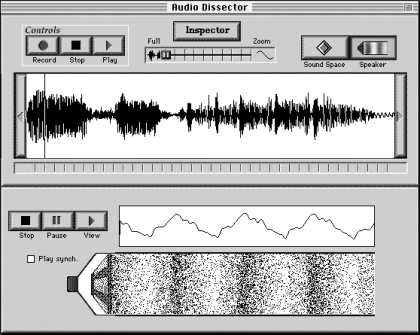
Se abbiamo a disposizione un numero maggiore di bit, potremo rendere più fine la griglia, oppure aumentare il numero dei colori, o magari (se possiamo permettercelo) fare tutte e due le cose insieme. Così, se ad esempio per ogni celletta decidiamo di 'spendere' 8 bit (e dunque 1 byte) anziché 1 bit soltanto, anziché usare solo il bianco e nero potremo codificare 256 colori diversi (giacché come abbiamo visto le possibili combinazioni di '0' e '1' nelle nostre 8 cellette sono proprio 256; quando si parla di immagini 'a 256 colori' o 'a 8 bit' ci si riferisce proprio a un'immagine la cui palette di colori - ovvero l'insieme dei colori utilizzati - è codificata in questo modo); se di bit ne possiamo spendere 16, avremo a disposizione 65.536 colori diversi, e così via. Certo, con l'aumento della risoluzione e la crescita del numero dei colori codificati, il numero di bit necessario a rappresentare la nostra immagine sale molto: supponiamo di voler utilizzare una griglia di 800 colonne per 600 righe (è una risoluzione assai diffusa per i personal computer), e di destinare a ogni celletta, a ogni pixel, 24 bit (il che ci consentirà di distinguere la bellezza di oltre 16 milioni di sfumature di colore). I bit necessari per rappresentare una singola immagine diventano 800x600x24 = 11.520.000: una cifra di tutto rispetto!

Tuttavia, il progresso tecnologico (che - ricordiamolo - dipende non solo dall'ingegno umano, ma anche dalle altissime risorse economiche investite in un settore evidentemente considerato strategico) ci ha portato da una situazione in cui il risparmio di ogni singolo bit costituiva una priorità essenziale a una situazione in cui i bit sono sempre più 'economici'. I computer delle nuove generazioni dispongono così di veri e propri 'sottosistemi' interamente dedicati alla gestione della grafica, dotati di una memoria indipendente (in modo che la rappresentazione delle immagini non sottragga troppe risorse agli altri compiti nei quali il computer può essere impegnato) e man mano sempre più larga. Inoltre, sono stati fatti molti progressi nelle tecnologie per il 'risparmio' dei bit: si tratta delle cosiddette tecniche di compressione, che sfruttano complessi algoritmi matematici, ad esempio considerando la diversa frequenza dei colori in un'immagine, per ridurre il numero di bit necessari alla sua rappresentazione. Come risultato, nella rappresentazione di immagini fisse è ormai possibile arrivare al livello del fotorealismo: griglie talmente fitte, e codifica di una 'palette' talmente ampia di colori, da rendere sostanzialmente indistinguibile all'occhio umano l'immagine (digitale) visualizzata attraverso il computer da quella (analogica) risultato di una fotografia tradizionale.

Ed i suoni?

Abbiamo dunque risolto il problema della rappresentazione binaria delle immagini. Ma come la mettiamo con i suoni? In questo caso, la trasformazione del dato analogico in dato digitale si basa su un processo di 'segmentazione' ('campionamento') - il più raffinata possibile - dell'onda sonora di partenza. E' possibile rappresentare in molti modi un'onda sonora, ma la rappresentazione più comoda è attraverso una funzione, simile a quella rappresentata al centro della figura 4. Con un procedimento non troppo dissimile da quello già considerato a proposito della grigliatura in pixel di una immagine, questa funzione può essere 'segmentata' in regioni abbastanza piccole da poter essere considerate come se si trattasse di singoli punti. Ognuno di questi punti sarà identificato dai suoi valori sugli assi del piano cartesiano, e questi valori, naturalmente, sono dei numeri: sappiamo dunque bene come rappresentarli attraverso una codifica binaria. Ecco allora che la successione di questi valori (assieme alle necessarie informazioni sullo spettro delle frequenze considerate e sulla 'frequenza di campionatura', che ci dicono in sostanza quanto è esteso lo spettro sonoro considerato e quanto è accurata la nostra segmentazione della funzione d'onda, ovvero quanto 'fitta' è la nostra griglia) ci fornisce quella rappresentazione numerica, e dunque quella digitalizzazione dell'onda sonora, che stavamo cercando (gli strumenti pratici da utilizzare in questo caso sono discussi nella scheda "Le tecnologie di digitalizzazione"). Naturalmente, un sonoro stereofonico ci imporrà di considerare separatamente le onde sonore dei due canali corrispondenti agli altoparlanti di destra e di sinistra.

Figura 4 - Diverse rappresentazioni del suono. L'immagine è tratta dal software 'AudioDissector' utilizzato nel Computer as Learning Partner Project della University of California

at Berkeley

Nel campo dei suoni, la qualità ottenibile attraverso la digitalizzazione è già molto alta, tanto che ormai la resa audio dei Compact Disc musicali (che contengono informazione in formato digitale) ha superato quella dei vecchi dischi di vinile (nei quali l'informazione sonora era registrata in formato analogico). Inoltre, la produzione di nuove copie di un brano in formato digitale non implica una perdita di qualità (la copia è perfettamente uguale all'originale, dato che i dati numerici che vi sono codificati sono esattamente gli stessi), mentre sappiamo che nel campo dell'analogico ogni 'passaggio' di copiatura introduce disturbi e distorsioni che comportano un peggioramento della qualità sonora.

Anche il video diventa digitale

Armati dei risultati conseguiti con suoni e immagini, possiamo affrontare adesso il problema della digitalizzazione dei filmati, ovvero di immagini in movimento con accompagnamento sonoro. Se pensiamo a come è fatta una vecchia pellicola cinematografica, ci risulterà chiaro che un filmato altro non è se non una successione di fotogrammi (ciascuno dei quali corrisponde a un'immagine statica), accompagnata da una banda sonora. Ma a questo punto sappiamo come digitalizzare tanto le immagini che corrispondono ai singoli fotogrammi, quanto il sonoro che le accompagna. Certo il numero di bit impiegati nell'operazione aumenta vorticosamente. Per essere esatti, aumenta in funzione di almeno cinque fattori: il numero di bit necessari alla codifica sarà infatti tanto maggiore quanto più lungo è il filmato, quanto maggiore è la sua risoluzione grafica (e cioè quanto più fitta è la griglia che usiamo per digitalizzare i singoli fotogrammi), quanto più ampia è la 'palette' di colori utilizzata, quanto maggiore è il numero di fotogrammi (o frame) per secondo, e quanto migliore è la qualità del sonoro (ovvero la frequenza di campionatura). Una bassa risoluzione grafica rende il filmato quadrettato e indistinto, una 'palette' troppo ristretta rende poco realistici i colori visualizzati, un numero troppo basso di frame per secondo produce un filmato 'a scatti' e poco fluido, e una frequenza di campionatura audio troppo bassa pregiudica la qualità del sonoro. Come si vede, i fattori da considerare sono davvero tanti: per quanto la nostra 'disponibilità di bit' sia notevolmente aumentata col tempo, e nonostante il fatto che proprio nel campo delle immagini in movimento le tecniche di compressione abbiano fatto passi da gigante, il cosiddetto 'full motion video' digitale (la capacità cioè di rappresentare a pieno schermo immagini in movimento, con una risoluzione e con una fluidità simile o migliore rispetto a quelle televisive) è un traguardo raggiunto solo di recente (cf. dispensa 7, scheda "TV digitale") , e non in tutti i casi. Ad esempio, i video tratti dalle videocassette di questo corso sono presenti anche sul CD-ROM, solo in forma molto compressa e di bassa qualità, altrimenti occuperebbe molto più 'spazio', molti più bit, di quello disponibile su un singolo CD. Per quanto riguarda il video digitale, dunque, gli ulteriori prevedibili progressi nelle capacità di memoria e nella velocità di elaborazione dei computer potranno ancora portare a un significativo miglioramento della qualità.

Possiamo dirci soddisfatti: armati solo degli '0' e '1' della codifica digitale abbiamo affrontato tipi di informazione molto diversa - dai numeri al testo scritto, dai suoni alle immagini e al video in movimento - e siamo riusciti a rappresentarli tutti. Possiamo capire - e considerare in certa misura quasi profetico - lo slancio delle parole con le quali all'inizio del '700 il filosofo tedesco Gottfried Willhelm Leibniz (vedi scheda), che può essere considerato l'inventore del calcolo binario, parlava della sua scoperta. Leibniz vedeva nella notazione binaria "un'immagine della creazione, ovvero dell'origine delle cose da Dio e dal nulla", e sosteneva: "il calcolo binario, che utilizza lo '0' e l''1', a ricompensa della sua maggiore lunghezza è il più fondamentale per la scienza, ed è all'origine di nuove scoperte (...) la cui ragione è che allorché i numeri sono ridotti ai principi più semplici, e cioè allo '0' e all''1', appare ovunque un ordine meraviglioso"^[1].

Figura 5 - Un manoscritto (1705) di G.W. Leibniz contenente la descrizione del calcolo binario

Ma torniamo al concetto di informazione.

Per rispondere pienamente al compito che ci eravamo proposti, tuttavia, restano ancora da affrontare due punti estremamente importanti. Il primo è forse un po' tecnico, e ci fa tornare alla definizione di informazione. Ricorderete che abbiamo iniziato il nostro discorso proprio dal tentativo di trovare una definizione rigorosa di questo concetto, pur avendo ben presente che per farlo avremmo dovuto sacrificare alcune fra le molte connotazioni abitualmente associate al nostro uso generico del termine 'informazione'. Abbiamo poi osservato come in molti casi il concetto di informazione sia collegato al concetto di scelta fra più alternative. Il successo ottenuto nel compito di codificare in formato binario 'informazioni' di tipo diverso (testi, suoni, immagini...) è in buona parte dovuto proprio alla applicazione di questo principio. Quando codifichiamo un testo, 'scegliamo', carattere per carattere, la codifica esatta fra le 256 alternative forniteci dalla nostra tabella di codifica: il 'peso' informativo di ogni carattere del nostro testo è così pari a 1 byte, ovvero a 8 bit. Quando codifichiamo un'immagine, il suo 'peso' informativo dipende da un lato dalla sua risoluzione (maggiore è la risoluzione, più informativa sarà l'immagine), dall'altro dalla 'palette' di colori usata (anche qui, più sfumature di colore siamo in grado di rappresentare, più informativa sarà l'immagine). E, nuovamente, entrambi questi fattori hanno a che fare con delle scelte fra più alternative: col crescere della risoluzione, cresce il numero di pixel che abbiamo a disposizione per rappresentare l'immagine, e col crescere della 'palette' cresce il numero di colori fra i quali possiamo scegliere per ogni pixel.

Come risulta dalla definizione che ne abbiamo dato, quando diciamo che il bit è una unità di misura della quantità di informazione ci riferiamo proprio a questo senso 'tecnico' di informazione, collegato alla scelta fra alternative: più alternative abbiamo a disposizione, più informativa sarà la nostra scelta, e maggiore il numero di bit necessario a esprimerla. Questa idea - formulata in maniera rigorosa nel 1948 dall'americano Claude Shannon (vedi scheda) - è alla base della disciplina scientifica denominata appunto teoria dell'informazione. E c'è una lezione che possiamo trarre dalla nostra capacità di rappresentare attraverso la codifica digitale tipi diversi di informazione: una definizione di informazione basata sull'idea che la quantità di informazione cresca col crescere delle alternative fra le quali possiamo scegliere, può forse aiutarci a comprendere meglio anche altri, più 'intuitivi' (ma magari meno chiari) significati che attribuiamo a questo termine. Anche per questo, può essere utile andare a dare un'occhiata un po' più da vicino al modo in cui il concetto di informazione è definito nell'ambito della teoria dell'informazione: è quello che facciamo in una delle schede di approfondimento.

Convergenza al digitale

Il secondo punto sul quale occorre soffermarsi è assolutamente fondamentale, e ha a che fare in fondo con la stessa ragion d'essere di questo corso. Abbiamo visto e - speriamo - capito insieme, almeno per sommi capi, cos'è l'informazione in formato digitale. Ma non abbiamo ancora capito - o almeno, non abbiamo ancora discusso - il primo degli interrogativi posti all'inizio della lezione: perché la trasformazione in formato digitale dell'informazione sia così importante, tanto da rappresentare una delle chiavi di lettura principali di questa fine millennio, e da far parlare di rivoluzione digitale. Per quello che abbiamo detto finora, potrebbe in fondo trattarsi di una tecnica di rappresentazione come un'altra, utile magari per capire come funzionano i computer quando lavorano con testi, suoni o immagini, ma priva di una particolare portata 'rivoluzionaria'. In sostanza, le nozioni che abbiamo fornito potrebbero sembrare utili solo a soddisfare, almeno in parte, una curiosità tecnica.

Il seguito di questo corso avrà fra i suoi compiti principali proprio quello di rispondere a questo interrogativo. Ma la più importante delle risposte può essere anticipata subito, almeno nelle sue linee generali. Ci sono infatti due fattori che rendono così potente la rappresentazione in formato digitale delle informazioni.

Innanzitutto, il computer non è solo o principalmente uno strumento per rappresentare in forma statica i nostri dati, la nostra informazione: al contrario, è uno strumento potentissimo per lavorare su questa informazione, conservandola, elaborandola, e, se lo si desidera, trasmettendola a distanza attraverso le reti telematiche. Nella prossima lezione, vedremo più da vicino come è fatto un computer, e in che modo funziona: potremo così capire meglio - cosa che cercheremo di fare nelle lezioni successive - alcuni dei molti modi in cui è possibile utilizzare, concretamente, l'informazione in formato digitale.

In secondo luogo, la disponibilità di un unico linguaggio (la codifica digitale) per rappresentare informazione di molti tipi diversi, associata alla disponibilità di un unico strumento (il computer) per gestire ed elaborare questa informazione, permette un livello di integrazione fra codici diversi totalmente nuovo. Tradizionalmente, i supporti utilizzati per i testi scritti (nel mondo 'gutenberghiano' nel quale abbiamo vissuto finora, soprattutto la carta stampata: libri, giornali, riviste...) erano diversi, nelle tecnologie impiegate e nei modi di fruizione, dai supporti utilizzati per i suoni (pensiamo ad esempio a dischi e audiocassette), da alcuni di quelli usati per le immagini (negativo fotografico, diapositive...) o per i filmati (pellicola cinematografica, videocassetta...). L'universo comunicativo era popolato da media tecnologicamente assai diversi (si pensi alle differenze esistenti fra stampa, radio, televisione, cinema...), la cui integrazione poteva risultare - e di fatto spesso risultava - assai difficile, se non del tutto impossibile.

Con il digitale, questa situazione - sulla quale torneremo anche nella sesta dispensa cercando di definire meglio termini quali 'comunicazione' e 'medium' - cambia radicalmente. Informazioni di tipo diverso vengono 'scritte' attraverso lo stesso linguaggio di base (il linguaggio dei bit, le nostre lunghe catene di '0' e '1') e gestite attraverso lo stesso strumento di base (il computer). Un CD-ROM, o il disco rigido di un computer raggiungibile attraverso la rete Internet, possono così offrire insieme testi, suoni, immagini, video in movimento; un 'telegiornale digitale' può essere fatto di servizi filmati, ma anche di testi scritti (da leggere e magari da stampare sulla stampante del nostro computer, e sui quali potremo effettuare ricerche), e potrebbe essere ricevuto attraverso un qualunque canale in grado di trasmettere informazione in formato digitale (cavi, satelliti, onde radio... torneremo su tutto ciò nella terza dispensa; su un CD (e dunque su un unico medium) un brano sonoro può essere accompagnato dal testo che lo descrive e dalle immagini della sua esecuzione; una trasmissione digitale via satellite può contenere immagini, ma anche testi, o magari programmi per computer; assieme alla fotografia di un matrimonio possiamo conservare l'audio del 'sì' degli sposi. E, grazie alle capacità che ha il computer di gestire informazione in formato digitale, queste informazioni possono essere fruite in maniera interattiva, ad esempio scegliendo al momento quali informazioni ci interessa ricevere.

Sui concetti di multimedialità e interattività avremo occasione di soffermarci in seguito: ma il dato di fondo che interessa sottolineare è che la convergenza al digitale (è così che ci si riferisce spesso al progressivo trasferimento verso il formato digitale di tipologie di informazione tradizionalmente collegate a media diversi: anche su questo termine torneremo nella settima dispensa) rende possibile una integrazione strettissima e totalmente inedita fra codici e linguaggi che eravamo abituati a considerare lontani. E, per questa via, rende possibile forme di comunicazione nuove, le cui caratteristiche e potenzialità stiamo appena iniziando ad esplorare.

Lezione n. 01

Verso il digitale

di Gino Roncaglia

Argomenti associati:

Argomenti trattati nella lezione 01:

Premessa