Nella dispensa
precedente abbiamo visto in che modo nell'ambito dell'intelligenza artificiale
si sia tentato di riprodurre sul computer alcune delle facoltà simboliche che
caratterizzano il comportamento intelligente, come l'uso del linguaggio
naturale e l'organizzazione della conoscenza sui fatti del mondo mediante
complesse strutture rappresentazionali. Ma evidentemente questi due domini,
per quanto importanti, non esauriscono l'insieme di facoltà che attribuiremmo
ad un essere intelligente. Infatti un agente intelligente deve anche esser in
grado di usare le conoscenze di cui è dotato per elaborare altre conoscenze,
per orientare il suo comportamento e per risolvere problemi di varia natura.
Sin dagli anni cinquanta molti ricercatori e studiosi di intelligenza
artificiale hanno rivolto la loro attenzione proprio a questo tipo di
facoltà, cercando di sviluppare dei programmi che fossero in grado di
effettuare ragionamenti e di affrontare problemi complessi.
Per capire in che modo si sia tentato di sviluppare
programmi in grado di ragionare e di risolvere problemi, esaminiamo questi tre
casi: un matematico che debba dimostrare un teorema, un giocatore di scacchi nel
corso di una partita e un normale individuo che debba scegliere che modello di
computer acquistare.
Il matematico parte da un insieme di conoscenze preesistenti
(tutti i teoremi della matematica dimostrati) e - applicando alcune regole o
conoscenze operative - cerca di dedurre da esse un nuovo teorema (il quale a sua
volta andrà ad aumentare le conoscenze). Nel fare questo procede per tentativi,
esplorando molte possibili strade di dimostrazione prima di individuare quella
giusta. Allo stesso modo il giocatore di scacchi di fronte ad una situazione di
gioco cerca di prevedere le conseguenze di ogni possibile mossa ragionevole
sfruttando la sua conoscenza delle regole del gioco e la sua esperienza. Infine
anche il nostro compratore cerca di acquisire la maggiore quantità possibile di
informazioni per valutare tutti i pro e i contro delle varie scelte di acquisto
che ha a disposizione, prendendo in considerazione fattori complessi come la sua
disponibilità finanziaria, l'utilità di una configurazione piuttosto che di
un'altra per la sua attività professionale o ricreativa etc.
Tutti e tre questi casi, se osservati in modo astratto,
presentano alcuni tratti in comune. Sembra insomma che vi sia un modello
generale di ragionamento soggiacente a queste attività. L'analisi di questo
modello e la sua riproduzione mediante sistemi informatici è il dominio di
molte ricerche che si collocano nell'ambito intelligenza artificiale e che
vengono di norma rubricate sotto le etichette di soluzione di problemi (problem
solving), dimostrazione automatica, ricerca selettiva. Naturalmente ognuna di
queste ricerche ha degli aspetti peculiari legati al particolare oggetto di
ciascuna di esse. Tuttavia si può individuare un corpo comune di metodologie e
di strumenti. Questo corpo comune consiste nella ricerca di una serie di
procedimenti generali per la risoluzione di problemi formalmente definibili. Per
capire di cosa si tratti, cominciamo con un esempio di 'ricerca della soluzione
di un problema' piuttosto comune e banale.
Immaginiamo che Marco sia in procinto di uscire di casa. Proprio
mentre sta per aprire la porta si accorge di avere perduto le chiavi della sua
automobile. Egli è tuttavia sicuro che le chiavi siano da qualche parte nel suo
piccolo appartamento di tre stanze. Si mette così a cercarle. Per evitare di
girare a vuoto, però, decide di procedere in modo sistematico nella sua
ricerca. Inizia così a cercare dall'ingresso. Naturalmente anche per effettuare
la sua ricerca nella stanza di ingresso adotta il medesimo approccio
sistematico. Si mette pertanto ad esplorare ogni singolo mobile presente
nell'ingresso, e per ogni singolo mobile guarda in ogni possibile cassetto,
piano o anta. Poiché la ricerca nell'ingresso non ha avuto esito, passa in
cucina. Anche qui guarda prima sul tavolo, poi sul frigorifero, poi sul piano di
cottura. Non avendo ancora trovato le chiavi si mette ad esplorare l'ultima
stanza, quella da letto, essendo ormai sicuro che le chiavi debbano essere li
dentro. Ovviamente anche nella camera da letto adotta la sua strategia
sistematica: comodino, cassetto del comodino, superficie del letto, sotto il
letto…
Lasciamo il nostro amico alla sua ricerca e proviamo ad
analizzare il suo comportamento. Il problema in questione è la ricerca delle
chiavi. Obiettivo della ricerca, ovviamente, è trovare le chiavi. Le possibili
soluzioni al problema nel momento iniziale della ricerca sono tutti i luoghi in
cui le chiavi possono essere riposte. Chiamiamo questo lo spazio del problema.
Per conseguire l'obiettivo Marco ha iniziato ad esplorare in modo sistematico
tutte le possibili soluzioni suddividendo lo spazio del problema in modo
gerarchico. Per ogni passo della sua ricerca ha naturalmente verificato se
l'obiettivo non fosse conseguito.
Un procedimento di ricerca come questo, può facilmente essere
rappresentato mediante un cosiddetto grafo ad albero. Un grafo ad albero è
costituito da un insieme di punti o nodi, connessi da segmenti orientati (cioè
dotati di un verso di percorrenza) e tale che esiste un solo nodo (detto radice)
al quale non arriva nessun segmento. Se esistono dei nodi dai quali non parte
nessun segmento, essi sono detti nodi terminali o foglie. Per associare un
albero ad un processo di soluzione di un problema come quello che abbiamo visto
è sufficiente associare ogni singolo passo della ricerca con un nodo.
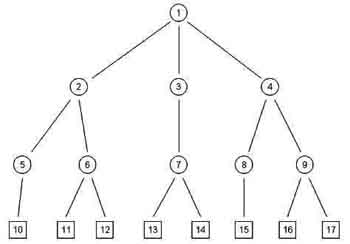
Figura 1 - Il grafo ad albero che
rappresenta il processo di ricerca di una soluzione
La ricerca di una soluzione corrisponde alla esplorazione dei
percorsi che legano i nodi dell'albero finché non si raggiunge un nodo foglia
che rappresenta lo stato finale o obiettivo della ricerca.
Ci sono due cose interessanti che possiamo capire grazie a
questo modo di rappresentare la ricerca della soluzione di un problema. In primo
luogo esso può essere applicato a moltissimi problemi di ambito diverso. Ad
esempio potremmo rappresentare allo stesso modo la ricerca del migliore
investimento da fare in borsa. O la scelta della mossa migliore durante una
partita di scacchi. In secondo luogo ci accorgiamo che è possibile seguire
diverse strategie nella ricerca delle soluzioni di un problema, ovvero diversi
modi di esplorare l'albero.
Le due principali sono la ricerca in profondità
(depht-first) e
la ricerca in ampiezza (breath-first). Nella ricerca in profondità ogni
percorso viene esplorato sistematicamente (in genere a partire da sinistra) fino
ad arrivare ad una foglia. Se non si è trovata una soluzione si torna indietro
fino alla prima biforcazione e si ripete l'operazione. Ad esempio nell'albero in
figura la ricerca in ampiezza procederebbe in questo modo: Prima si esplorerebbe
il percorso 1-2-5-10. In caso di esito negativo dal nodo 10 si tornerebbe al 2
per esplorare i percorsi 2-6-11 e 2-6-12. Se anche questa ricerca avesse un
esito negativo si tornerebbe fino a 1 per esplorare i percorsi passanti per 3.
Il processo continuerebbe fino al raggiungimento della soluzione. Per contro
nella ricerca in ampiezza vengono valutati prima tutti i rami che partono da un
dato nodo (ad esempio 1-2, 1-3, 1-4) e poi si scende di un livello e si
ricomincia il processo. Ciascuna di queste due strategie presenta dei lati
negativi e dei lati positivi. Per la ricerca in profondità, ad esempio, se
l'albero scende per molti livelli e la soluzione si trova in uno dei nodi alti
dei rami più a destra si perde moltissimo tempo per esplorare lunghi percorsi
improduttivi. Inoltre se un percorso non arriva mai ad una foglia (l'albero
cioè è infinito) il programma continuerebbe ad esplorarlo egualmente senza
fermarsi. D'altra parte se una soluzione si trova in un nodo molto basso, è la
ricerca in ampiezza a rivelarsi inefficiente.
Un altro aspetto da considerare è che alcuni problemi (è
questo il caso della esplorazione di tutte le possibili mosse di una partita di
scacchi per trovare la mossa giusta) generano un numero enorme di nodi. In
questo caso una esplorazione sistematica lungo tutti i percorsi potrebbe
richiedere tempi enormi. Per questi motivi i ricercatori impegnati nell'ambito
del problem solving e della dimostrazione automatica hanno cercato di elaborare
delle strategie di ricerca selettiva, mediante le quali un programma potesse
limitare in anticipo i percorsi da esplorare per trovare una soluzione. Queste
strategie sono denominate euristiche.
Uno dei procedimenti euristici più noti è l'analisi
mezzi-fini,
formalizzata da Allen Newell, Cliff Shaw e Herbert Simon durante lo sviluppo di
un programma battezzato modestamente General Problem Solver (GPS, o 'solutore
generale di problemi'). Nell'analisi mezzi-fini la ricerca procede in questo
modo. Si prende in considerazione lo stato iniziale del problema e il suo
obiettivo, cercando di individuare in che cosa consista la differenza. Poi si
applicano una serie di regole di trasformazione per cercare di ridurre tale
differenza: questo equivale al darsi una sorta di obiettivo parziale. Una volta
conseguito l'obiettivo parziale si comincia da capo finché lo stato del
problema non coincida con l'obiettivo dato. Secondo Newell, Shaw e Simon, questo
tipo di ragionamento euristico sarebbe alla base del ragionamento umano.
In realtà il GPS, e i principi su cui era basato, si sono
rivelati troppo semplicistici. Come mette in evidenza Haugeland, due in
particolare sono le idee ingannevoli (J. Haugeland, Intelligenza Artificiale,
Bollati Boringhieri 1988, p. 168 e seg.). La prima è la tesi che malgrado le
diversità di superficie tutti i problemi, o almeno tutte le strategie di
soluzione dei problemi, siano sostanzialmente equivalenti. Ben presto ci si è
resi conto, al contrario, che ogni classe di problemi ha delle euristiche
specifiche che si applicano esclusivamente al dominio di quei problemi. La
seconda è la convinzione che la formulazione di un problema e del suo dominio
nei termini formali richiesti dai programmi di problem solving sia tutto sommato
un compito semplice. Invece il vero 'problema' nella risoluzione dei problemi
consiste proprio nel trovare il modo migliore, più efficiente e, perché no,
più elegante per formularlo.
Molti dei nostri lettori avranno sicuramente visto il film di
Stanley Kubrick 2001 Odissea nello spazio. Uno dei protagonisti del film,
ricorderete, è il computer HAL 9000. HAL è un computer dotato di una
stupefacente intelligenza: è in grado di conversare amabilmente in linguaggio
naturale, di esprimere giudizi su opere d'arte, di interpretare lo stato d'animo
dei suoi compagni di viaggio umani, oltre che di governare da solo l'astronave.
In una sequenza del film, viene messa in scena una partita di
scacchi: una partita tra HAL e Dave, uno degli astronauti, che viene
naturalmente vinta dal computer. Perché Kubrick decise di inserire quella
sequenza nel film? Perché la vittoria di HAL al gioco degli scacchi poteva dare
una idea assai chiara di quanto egli fosse intelligente.
Infatti il gioco degli scacchi, nella percezione comune, è
considerato il gioco intelligente per eccellenza. Sebbene si tratti di un gioco,
esso richiede una elevata capacità di ragionamento logico e una grande
quantità di conoscenze. Non a caso, sin dalle origini dell'intelligenza
artificiale moltissimi ricercatori hanno speso il loro ingegno nel tentativo di
realizzare un programma che fosse in grado di giocare a scacchi. E soprattutto
che fosse in grado di giocare allo stesso livello dei grandi maestri.
La storia degli scacchi al computer ha raggiunto il suo culmine
un paio di anni fa, quando per la prima volta un computer è stato in grado di
sconfiggere il più grande giocatore vivente, Gary Kasparov. Protagonista di
questo storico risultato è stato Deep Blue, un computer progettato e
programmato nei laboratori di ricerca della IBM. Kasparov e Deep Blue si sono
scontrati due volte. Il primo match si è svolto nel febbraio 1996. In quella
occasione Kasparov riuscì a sconfiggere il suo sfidante artificiale senza
troppa fatica. Ma nella rivincita, che si è svolta nel maggio del 1997, è
finalmente avvenuto ciò che si attendeva da anni: Deep Blue è riuscito a
vincere due partite e a pareggiarne tre, battendo Kasparov.
Deep Blue è un computer particolarmente potente. si tratta
infatti di una cosiddetta macchina parallela. Come sappiamo ogni computer di
norma è dotato di una unità centrale di calcolo, o CPU, che ne rappresenta il
cervello logico e matematico. Nelle macchine parallele, come Deep Blue, i
processori sono molteplici, e lavorano tutti insieme, in parallelo appunto. Ogni
singolo processore esegue una parte dei calcoli necessaria a risolvere un
problema. In questo modo si possono raggiungere potenze di calcolo elevatissime.
Nel caso di Deep Blue, inoltre, alcuni di questi processori erano stati
progettati in modo speciale per affrontare il tipo di problemi posti dal gioco
degli scacchi.
Ma perché gli studiosi di intelligenza artificiale hanno
dimostrato così tanto interesse (e hanno speso tante energie e finanziamenti)
verso il gioco degli scacchi? Una ragione la abbiamo già citata: si tratta di
un gioco che viene considerato un esempio tipico di attività intelligente.
Dunque, riuscire a creare un computer in grado di giocare a scacchi, e di
battere un esperto giocatore umano, rappresenta un buon successo per l'IA.
Ma ci sono almeno due altre ragioni che rendono gli scacchi
così interessanti. In primo luogo si tratta di un gioco in cui ci sono un
insieme limitato di elementi distinti (le pedine) e delle regole molto precise
che specificano quali mosse si possono fare. Ad esempio l'alfiere si può
muovere solo in diagonale. Infine sappiamo con certezza quando il gioco finisce.
Un gioco come questo, come sappiamo, può essere sicuramente giocato da un
computer.
Progettare un programma che sappia giocare a scacchi, dunque, a
prima vista non è così complicato. Basta rappresentare le pedine mediante un
insieme di simboli, e poi tradurre le regole del gioco in una serie di regole
per manipolare tali simboli. A questo punto il programma è in grado di
calcolare per ogni mossa tutte le possibili contromosse dell'avversario e per
ognuna di esse tutte le sue possibili contromosse, e così via. Se il programma
potesse veramente operare in questo modo riuscirebbe senza dubbio a trovare la
mossa giusta per ogni turno di gioco. Ma quante sono le possibili mosse di un
partita di scacchi?
In media per ogni turno un giocatore dispone di 35 alternative.
Dunque per valutare tutte le possibili conseguenze di un sola mossa occorre
verificare 35 x 35, cioè 1225 possibilità. Questo significa che per valutare
le conseguenze dopo due mosse bisogna analizzare più di un milione di
possibilità. Per farla breve, per prevedere con questo metodo tutte le mosse di
una partita bisognerebbe valutare un numero come 10120 possibilità. Un fenomeno
di crescita come questo viene chiamato esplosione combinatoria. Anche il
computer più veloce che possiamo immaginare impiegherebbe miliardi di miliardi
di anni per fare questo calcolo: e il nostro universo ha solo 15 miliardi anni!
Evidentemente programmare un computer in questo modo non avrebbe
senso. E soprattutto, è chiaro che un uomo che gioca a scacchi non ragiona in
questo modo. Ben presto gli studiosi che si sono applicati a questo problema si
sono resi conto che bisognava fornire al computer delle strategie di gioco che
gli permettessero di limitare il numero di mosse e contromosse da esplorare.
Queste strategie non garantiscono la certezza assoluta della vittoria: esse
indicano solo le strade ragionevolmente più interessanti per trovare la mossa
giusta. Sono dunque delle euristiche per l'esplorazione dello sterminato
(praticamente infinito) albero che rappresenta tutte le possibili mosse di una
partita.
Secondo molti teorici dell'intelligenza artificiale anche un
uomo dotato di un livello poco più che minimo di conoscenza degli scacchi usa
delle euristiche quando gioca. I grandi maestri, dunque sono coloro che hanno
elaborato le euristiche più efficaci.
Ma come sappiamo il ragionamento euristico ha dimostrato di
avere una portata molto più vasta. E questa è la terza ragione per cui gli
scacchi hanno destato tanto interesse. La capacità di giocare bene a scacchi
può essere vista come esempio di una capacità ben più generale: quella di
affrontare e risolvere problemi complessi e di scegliere di volta in volta le
soluzioni migliori. E questa capacità fa senza dubbio parte di ciò che
chiamiamo essere intelligenti.
Va detto comunque che, anche se programmi come quello utilizzato
da Deep Blue incorporano componenti euristiche, siamo ancora molto lontani dal
poter dire di aver costruito una macchina dalla 'intelligenza scacchistica'
paragonabile a quella di un giocatore umano. Il punto di forza di Deep Blue -
come del resto di tutti i programmi per il gioco degli scacchi - resta infatti
la capacità di calcolo, la 'forza bruta'. Rispetto al giocatore umano, in grado
di individuare immediatamente le strategie più promettenti e di limitare
fortemente il numero di mosse analizzato, le capacità euristiche del computer
restano grossolane: quanto basta per limitare in qualche modo l'esplosione
combinatoria, e renderla compatibile con le capacità di calcolo della macchina.
Insomma, il computer è in grado di compensare la minore 'intelligenza' con la
capacità di analizzare un numero assai maggiore di mosse, molto più
velocemente di un uomo. La sconfitta di Kasparov indica solamente che
l'equilibrio di questi due fattori si è ormai spostato (o si sta spostando) a
favore della macchina, ma non che il computer sia diventato un giocatore
dall'intelligenza scacchistica maggiore di quella di un uomo.
I sistemi
esperti
Le ricerche nell'ambito del problem
solving, insieme a quelle
sulla rappresentazione delle conoscenze, sono alla base della creazione dei
sistemi esperti. I sistemi esperti rappresentano la più importante (e forse la
sola vera) applicazione dell'intelligenza artificiale che ha avuto una ricaduta
pratica (anche e soprattutto a livello commerciale).
In estrema sintesi, con il termine 'sistema esperto' si intende
un programma che è in grado di risolvere problemi complessi che rientrano in un
particolare dominio, con una efficienza paragonabile a quella di uno specialista
umano di quel settore. Ad esempio un sistema esperto potrebbe essere capace di
fare diagnosi mediche esaminando le cartelle cliniche (opportunamente
formalizzate) di un paziente; o potrebbe valutare tutti fattori di rischio e le
prospettive di guadagno di un determinato investimento finanziario.
Come viene realizzato concretamente un programma di questo tipo?
Di norma tutti i sistemi esperti hanno i seguenti componenti:
-
una base di conoscenza specialistica su un determinato
dominio, che rappresenta il sapere necessario ad affrontare e risolvere
problemi in quel campo. Ovviamente la base di conoscenza dovrà essere
opportunamente rappresentata nella memoria del calcolatore mediante uno dei
formalismi (o altri simili) che abbiamo visto nella terza dispensa parlando
di knwoledge representation;
-
un motore inferenziale che sia in grado di dedurre (o
inferire), a partire dalla base di conoscenza, le conclusioni che
costituiscono la soluzione a un dato problema che rientra nel dominio. Il
motore inferenziale, che è il vero cuore del programma, funziona applicando
alla base di conoscenze una serie di procedure euristiche simili a quelle
sviluppate nell'ambito del problem solving. Tuttavia nella maggior parte dei
casi alle euristiche generali si affiancano delle euristiche specifiche per
l'argomento di cui il sistema si occupa. Infatti in ogni campo specialistico
un esperto umano è in grado di escludere immediatamente e senza valutarle
una serie di opzioni che sono manifestamente improduttive;
-
una interfaccia utente che è costituita da un insieme di
moduli informatici grazie ai quali un essere umano è in grado di interagire
con il programma ponendo domande e leggendo le risposte. In alcun casi
l'interfaccia utente può anche prevedere dei moduli di aggiornamento della
conoscenza, che consentono agli utenti di aggiungere nuovi elementi alla
base dati originale.
Il primo sistema esperto ad essere realizzato è stato
DENDRAL,
sviluppato da Feigenbaum nel 1965 e in grado di analizzare la struttura chimica
delle molecole organiche. Ma il vero punto di svolta nella storia di questi
programmi è rappresentato dalla creazione (sempre da parte di Feigenbaum
insieme a Buchanan e Shortliffe) di MYCIN, che risale al 1972. MYCIN è un
sistema specializzato nella diagnosi di malattie infettive, ed è
sorprendentemente abile. Per lavorare fa ricorso ad una base di conoscenza molto
dettagliata sulla sintomatologia di tutte le sindromi infettive conosciute, che
confronta con la cartella clinica e con dati sulla storia clinica del singolo
paziente sotto esame. Inoltre le euristiche di cui è dotato gli permettono non
solo di ipotizzare una diagnosi, ma anche di dare una valutazione sul grado di
esattezza delle diagnosi (o delle possibili diagnosi) proposte.
Le tecniche impiegate per realizzare MYCIN (che ha avuto un
grande successo commerciale ed è tuttora utilizzati in moltissimi ospedali,
soprattutto in ambito statunitense) hanno dato origine ad una vera e propria
famiglia di sistemi esperti: CASNET ad esempio è un sistema esperto per la
diagnosi del glaucoma; PUFF si occupa delle malattie polmonari (le sue diagnosi
si sono rivelate giuste nel 95% dei casi); un altro medico artificiale, questa
volta generico, è CADUCEUS; PROSPECTOR, invece è un sistema esperto in grado
di individuare la posizione di possibili giacimenti minerari sulla base di dati
geologici, ed è riuscito ad individuare miniere e giacimenti per un valore di
miliardi di dollari. Oltre che nell'ambito medico e in quello industriale,
questo genere di programmi si è rivelato molto utile anche nel campo
dell'insegnamento e della didattica.
Insomma i sistemi esperti costituiscono nel loro insieme una
delle applicazioni pratiche più interessanti dell'intelligenza artificiale.
Tuttavia, in un certo senso, il successo di queste applicazioni rappresenta una
misura delle difficoltà incontrate dall'intelligenza artificiale in senso
forte. Un sistema esperto infatti, pur essendo molto abile nel suo campo, non
sarebbe mai in grado di applicare la sua abilità ad altri domini: il suo è una
specie di micromondo, solo un po' più ricco di quello in cui operava SHRDLU. E
soprattutto un sistema, per quanto possa essere esperto in medicina o geologia,
non riuscirebbe mai a trovare la soluzione ad un qualsiasi banale problema
quotidiano che ciascun essere umano risolverebbe con il solo buon senso.
La questione del
senso comune e il problema della cornice
Quando il progetto dell'intelligenza artificiale ebbe
inizio, nella metà degli anni 50, molti tra i suoi sostenitori si dissero
convinti che entro quaranta o cinquanta anni sarebbe stato possibile realizzare
dei programmi veramente intelligenti. In realtà le cose sono andate
diversamente, e le difficoltà incontrate in questa impresa si sono rivelate
assai più profonde e radicali di quanto non ci si aspettasse. E la difficoltà
maggiore non consiste tanto nel far fare ai computer cose 'difficili'. Come
abbiamo visto esistono computer che sanno giocare a scacchi come il più bravo
giocatore umano. Così come esistono moltissimi programmi in grado di dimostrare
teoremi matematici, o di risolvere problemi molto specialistici. Ma nessuno di
essi sarebbe in grado di comprendere i fatti più banali e ordinari della vita
quotidiana, come ad esempio andare a prendersi un caffè, o capire una
barzelletta.
Ma perché è così difficile fornire ad un computer
quell'insieme di conoscenze e capacità che chiamiamo senso comune e che ognuno
di noi acquisisce senza fare alcuno sforzo? Perché oggi un computer è in grado
di sconfiggere il campione del mondo di scacchi, ma non riuscirebbe mai a
districarsi in una normale situazione della vita quotidiana?
Malgrado le apparenze, i problemi implicati dal conferimento di
un barlume di senso comune ad un computer sono moltissimi e straordinariamente
complessi. Abbiamo visto, ad esempio, che i ricercatori hanno proposto diversi
modi per rappresentare la conoscenza sul calcolatore; ma quanta informazione
bisognerebbe dare al computer per permettergli di interpretare correttamente
tutte le possibili situazioni che gli vengono presentate? Sicuramente
moltissima, ma nessuno è stato finora in grado di stabilire esattamente quale e
a individuare dei sistemi per orientare il comportamento di una macchina in
situazioni reali.
Inoltre, ammesso che si riuscisse a formalizzare tutta la
conoscenza del senso comune , ben altra cosa sarebbe fare in modo che un
programma (magari in grado di controllare un robot) si dimostrasse sempre in
grado di selezionare dalla sua memoria la conoscenza giusta per una data
situazione, o di capire dal contesto quale conoscenze implicite utilizzare per
dare un senso ad un atto comunicativo. Un problema apparentemente simile a
quello della selezione delle conoscenze, ma in realtà ancora più complesso, è
il cosiddetto problema della cornice (in inglese frame problem, ma qui il
termine frame non ha nulla a che vedere con il formalismo ideato da Minsky), sul
quale si è accumulata una letteratura scientifica e filosofica ricchissima. Per
capire di cosa si tratti, usiamo una piccola storiella ideata da John Haugeland:
"C'erano una volta tre Scatole: Papà Scatola, Mamma Scatola e il piccolo
Baby Scatola. Papà Scatola stava sul pavimento al centro dello loro modesta
casetta, con Baby Scatola appollaiato sulla spalla; Mamma scatola sedeva
tranquillamente accanto alla porta. All'improvviso, sferragliando sulle sue
rotelline, entrò Cavodoro, tutta desiderosa di risolvere qualche problema. Si
guardò intorno e poi con somma cura spinse Papà scatola fino alla parete
opposta." (J. Haugeland, Intelligenza Artificiale, Bollati
Boringhieri 1988, p. 190)
Immaginiamo ora di porre queste tre domande al robot
'intelligente' Cavodoro:
-
Dov'è ora Papa scatola?
-
Dov'è ora Mamma scatola?
-
Dov'è ora Baby Scatola?
Cavodoro sa perfettamente dov'è Papa Scatola perché è lei che
lo ha spinto fino alla parete. Per quanto riguarda Mamma Scatola e Baby, non
avendoli toccati, il robot presumerebbe che siano rimasti dov'erano. Il fatto è
che la sua azione di spostare Papà Scatola ha avuto un effetto collaterale: lo
spostamento di Baby, poggiato sopra il papà. Dunque per rispondere alla terza
domanda il robot dovrebbe tenere conto di questo effetto collaterale. Il
problema è che i possibili effetti collaterali di una azione sono tantissimi.
Ad esempio:
-
Quando si è aperta la porta Baby è caduto per lo
spostamento d'aria;
-
Quando si è ha aperta la porta il gatto si è spaventato e
ha fatto un salto su Papà Scatola che ha fatto cadere Baby;
-
Quando si è aperta la porta la finestra si rotta;
-
…
Evidentemente, anche se il robot fosse dotato delle regole
necessarie per farlo, calcolare tutti i possibili effetti collaterali di una
azione sarebbe improponibile. Ma allora, in che modo selezionare tra questo
sterminato numero di conseguenze quelle rilevanti?
Naturalmente in una situazione semplice come quella della
famiglia di scatole non sarebbe difficile dare ad un programma la capacità di
tenere conto degli effetti collaterali rilevanti (ricordate SHRDLU?). Ma nella
vita reale l'impresa è molto più complicata. Ad esempio, se entriamo in una
casa e diamo una spinta al padrone di casa, egli potrebbe reagire, oppure la
moglie potrebbe chiamare la polizia, o potrebbe arrivare un vicino e fermarci.
Ogni nostra azione insomma ha una serie di conseguenze che ci costringono ad
aggiornare continuamente la nostra conoscenza. E talvolta questi aggiornamenti
sono radicali. Noi esseri umani siamo capaci di fare queste cose senza troppa
difficoltà e in pochi secondi sin dalla tenera età. Ma finora nessuno è stato
in grado di capire esattamente come questo avvenga e di trasformarlo in una
serie di regole euristiche che un computer potrebbe usare per aggiornare nel
corso del tempo le sue conoscenze sui fatti accidentali del mondo e sulle
conseguenze delle sue eventuali azioni.
|