Talvolta, quando ci mettiamo di fronte ad un computer e lo
osserviamo mentre esegue i suoi compiti, può accadere di avere l'impressione
che esso sia dotato di una specie di intelligenza. Tuttavia sappiamo che questa
impressione è sbagliata. Un computer, infatti, non fa altro che eseguire una
sequenza di istruzioni, esplicitate in un programma, in maniera meccanica. Senza
dubbio esistono programmi che possono eseguire operazioni molto complicate.
Persino un comune programma di videoscrittura può avere centinaia o migliaia di
comandi, alcuni dei quali possono apparire, specialmente all'occhio di un utente
inesperto, incomprensibili. Ma appena si acquista un po' di confidenza qualsiasi
programma, per quanto complicato, perde tutta la sua aurea di mistero. Non a
caso il computer viene considerato dalla maggior parte della gente solo un utile
strumento. E sicuramente nessuno riterrebbe che uno strumento, per quanto
complesso, sia dotato di intelligenza. D'altra parte nella considerazione
generale nemmeno gli esseri viventi più vicini a noi, come i cani, i gatti o le
scimmie, vengono ritenuti in possesso di vere e proprie capacità intellettive.
A questo punto dobbiamo affrontare un piccolo excursus filosofico (non sarà
l'unico, ma il tema lo richiede). Nella considerazione comune l'intelligenza
umana rientra tra quei fenomeni che trascendono il mondo fisico e le sue leggi.
Anche coloro che non professano alcuna credenza religiosa raramente sono
disposti ad accettare l'idea che il pensiero, la coscienza, il ragionamento
possano essere spiegati mediante qualche tipo di teoria scientifica. La
formulazione più esplicita (e famosa) di questa credenza la dobbiamo al
filosofo Cartesio, vissuto nel '600. Egli infatti, pur essendo stato uno dei
fondatori del moderno pensiero scientifico, quando arrivò a trattare il
problema della ragione umana non volle estendere anche ad essa la sua concezione
meccanicista. Sostenne così che la mente e la realtà materiale sono fatti di
due sostanze diverse, e che rispondono a leggi del tutto diverse.
Questa
visione, che prende il nome di dualismo, esercita tuttora un fascino notevole e,
come abbiamo rilevato, è condivisa anche a livello di senso comune. Essa
tuttavia va incontro ad una grossa difficoltà: se la mente è irriducibilmente
separata dalla materia (e dunque dal corpo), come è possibile che queste due
entità interagiscano? Il fatto che l'interazione esista è innegabile: quando
io penso di avere fame e decido di voler mangiare il mio corpo si alza, va in
cucina e mangia. La causa del movimento del mio corpo, dunque, è un mio
pensiero. Ma come può una sostanza immateriale esercitare una azione causale su
una sostanza materiale? Lo stesso Cartesio si rese conto di questa difficoltà,
e cercò di trovare una spiegazione, senza molto successo.
A questo punto non
restava che accettare un atto di fede (mente e corpo interagiscono, pur essendo
distinti, in virtù di un processo misterioso e inspiegabile) o risolvere il
dualismo in un senso o nell'altro. Alcuni filosofi scelsero di negare (in vari
modi) l'esistenza autonoma (o l'attingibilità) della realtà, dando vita alla
tradizione filosofica che prende il nome di idealismo. Altri pensatori invece,
cercarono di elaborare una teoria della mente che fosse compatibile con le leggi
della realtà materiale. Non possiamo soffermarci sulla evoluzione di questa
complessa vicenda intellettuale, durata oltre quattrocento anni. Tuttavia su una
cosa ci preme attirare l'attenzione dei nostri pazienti lettori: una delle idee
ricorrenti in molti pensatori della tradizione meccanicista è che il pensiero
(per la precisione il ragionamento, ma ai nostri fini non fa differenza) sia in
ultima analisi una forma di calcolo che la mente effettua manipolando qualche
tipo di simboli, o idee.
Questa idea (che abbiamo espresso in una forma assai
semplificata) pur non essendo immune da problemi teorici e aporie, ha
attraversato la tradizione culturale occidentale fino alla metà del nostro
secolo, quando si è incontrata con la nascente scienza dei calcolatori. Un
incontro decisivo: i computer infatti dimostravano che una macchina materiale
era in grado di effettuare calcoli, anche molto complessi, senza fare appello a
nessuna sostanza o influenza misteriosa o spirituale. Possiamo dunque chiudere
questa nostra (prima) parentesi filosofica e ritornare al nostro argomento
iniziale.
Abbiamo detto che quando attribuiamo intelligenza ad un computer che
esegue un comune programma, in realtà siamo preda di un abbaglio. Ma se fosse
corretto identificare il pensiero con una qualche forma di calcolo, non vi
sarebbe alcuna ragione di principio che impedirebbe di sviluppare programmi
tanto complessi e potenti da dotare veramente la macchina di un comportamento 'intelligente'.
Anzi potremmo anche spingerci oltre: non esiste nessuna ragione di principio per
cui un computer non possa avere una mente intelligente in tutto e per tutto
uguale a quella di un essere umano. Per conseguire tale obiettivo 'basterebbe',
per così dire, capire che genere di calcoli sono alla base della nostra mente,
e trasformarli in programmi per un computer. A partire dagli anni 50, con
l'emergere della nuova disciplina chiamata intelligenza artificiale, alcuni
scienziati e ricercatori si sono posti esattamente questo obiettivo.
Prima di procedere con la nostra trattazione
riteniamo opportuno fissare (nei limiti del possibile) alcuni termini di base.
Cominciamo proprio con 'intelligenza artificiale'. Di norma questo termine (che
viene comunemente contratto nell'acronimo 'IA') viene utilizzato per designare
una disciplina scientifica (talvolta considerata una branca della più generale
scienza dei calcolatori) il cui obiettivo può essere definito l'indagine sui
meccanismi soggiacenti alle facoltà cognitive degli esseri umani (come il
linguaggio, il ragionamento, la capacità di risolvere problemi, la percezione)
e la loro riproduzione mediante computer opportunamente programmati (in realtà
la limitazione allo studio delle facoltà cognitive degli esseri umani non è
condivisa da tutti i ricercatori di questa area. Sono anzi sempre più numerosi
gli studiosi che si occupano di studiare le facoltà cognitive di varie specie
animali). Il primo
ad usare l'espressione 'artificial intelligence' per indicare questo genere di
ricerche è stato John McCarty, durante uno storico convegno che si tenne nella
città statunitense di Dartmouth nel 1956. Non di rado lo stesso termine viene
usato per indicare la capacità di un computer o di un programma di eseguire
compiti intelligenti, o per qualificare un programma dotato di tali capacità
(ed esempio nell'espressione 'programma di intelligenza artificiale').
Con il
passare degli anni la disciplina designata come 'intelligenza artificiale' ha
subito una divisione in due aree, che si distinguono in relazione al senso del
termine 'riproduzione' che abbiamo usato nella precedente definizione.
La prima
area è la cosiddetta 'intelligenza artificiale forte', la quale ritiene che un
computer opportunamente programmato possa veramente essere dotato di una genuina
intelligenza, non distinguibile in nessun senso importante dall'intelligenza
umana. Come scrive John Haugeland: "La "IA" vuole solo originali:
macchine dotate di mente in senso pieno e letterale" (J. Haugeland,
Intelligenza Artificiale, Bollati Boringhieri 1988, p. 9). Alla base di questa
concezione vi è la teoria che anche la mente umana sia il prodotto di un
complesso insieme di procedimenti di calcolo, eseguiti dal cervello. Resta
naturalmente da stabilire rispetto a quale livello di descrizione cervelli e
computer possano essere considerati la stessa cosa (escludendo, almeno per ora,
il livello dell'hardware!); nondimeno i sostenitori dell'IA forte sono convinti
che un tale livello debba esistere. Questa area dell'IA è l'erede diretta della
tradizione filosofica cui accennavamo nella premessa.
La seconda area, per
contro, viene chiamata 'intelligenza artificiale debole'. Essa sostiene che un
computer opportunamente programmato possa solamente simulare i processi
cognitivi umani (o alcuni di essi), nello stesso senso in cui un computer può
simulare il comportamento di un evento atmosferico, o di una fissione nucleare
(nessuno direbbe che un computer che simula una tempesta è una tempesta!). In
questo caso dunque l'accento viene posto su ciò che un programma è in grado di
fare, senza fare assunzioni sul fatto che il modo in cui lo fa coincida ad un
qualche livello con i processi mentali umani. E d'altra parte non si pretende
che un programma, per quanto complesso ed efficiente, possa veramente dirsi un
esempio di 'mente'. Ovviamente i sostenitori di questa forma di IA sono
interessati anche alle molte applicazioni pratiche delle tecnologie che vengono
sviluppate nella loro disciplina.
Le due declinazioni dell'intelligenza
artificiale, pur differenziandosi profondamente rispetto agli assunti filosofici
di base e alle finalità, condividono metodologie, strumentazioni e tecnologie.
In particolare entrambe sostengono che per riprodurre e/o simulare un
comportamento intelligente al computer sia necessario elaborare informazione
(rappresentata da simboli discreti) mediante un programma . In questo senso esse
costituiscono quella che viene chiamata 'intelligenza artificiale classica' (o
più scherzosamente 'Good Old Artificial Intelligence', cioè 'Buona vecchia
intelligenza artificiale').
Ad essa si oppone una scuola più recente, che parte
da presupposti teorici affatto diversi: per ottenere un comportamento
intelligente mediante una macchina occorre riprodurre e/o simulare il
funzionamento del cervello a livello cellulare. Questa area di ricerca è
conosciuta come connessionismo, poiché cerca di ricostruire con strumenti
informatici la fitta rete di connessioni che legano le cellule neuronali.
Vale
la pena, infine, accennare ad un'altra disciplina: la scienza cognitiva. Si
tratta di una area di studi che si è venuta costituendo negli ultimi venti o
trenta anni grazie alla convergenza di esponenti di varie discipline
(intelligenza artificiale, linguistica, filosofia del linguaggio e delle mente,
psicologia cognitiva, neuroscienze), e il cui oggetto è lo studio dei sistemi
intelligenti, naturali o artificiali che siano. In un certo senso la scienza
cognitiva rappresenta l'erede della IA forte, soprattutto per la concezione che
i sistemi intelligenti (qualunque essi siano) siano fondamentalmente sistemi di
elaborazione dell'informazione che interagiscono con un ambiente complesso.
D'altra parte la compresenza di diverse tradizioni disciplinari ha fatto si che
in questa nuova area si riconoscessero anche molti studiosi fortemente critici
verso i fondamenti dell'IA.
In queste e nelle successive dispense del corso ci
soffermeremo su alcuni aspetti più strettamente legati alla intelligenza
artificiale propriamente detta. Tuttavia i lettori che fossero interessati ad
approfondire i temi qui trattati, troveranno nella bibliografia spunti relativi
a tutte le aree di ricerca che abbiamo fin qui menzionato.
La prima formulazione esplicita del fondamento teorico
dell’intelligenza artificiale si può forse rintracciare nel filosofo
empirista inglese Thomas Hobbes (vissuto nel 600), che nel Leviatano, il
suo libro più famoso, scrisse: “Ragionare non è nient’altro che
calcolare” (T. Hobbes, The Leviathan, Cap. V; tr. it T. Hobbes, Il Leviatano,
Editori Riuniti 1982). Con questa affermazione Hobbes intendeva dire che il ragionamento è una specie
di operazione interna condotta mediante la manipolazione di quelle che egli
stesso chiamò ‘particelle mentali’. Questa manipolazione, per Hobbes, era
molto simile alle operazioni che si effettuavano quando si calcolavano numeri
mediante un abaco. Si trattava, insomma di una serie di spostamenti delle
particelle mentali eseguiti in base a regole ben precise. Le particelle mentali,
infatti, erano concepite da Hobbes come dei minuscoli corpi fisici. Ma, a
differenza delle palline di un abaco, non si limitavano a rappresentare numeri:
potevano rappresentare molte altre cose.
Non seguiremo oltre quello che è stato definito ‘il
nonno dell’intelligenza artificiale’ nelle sue riflessioni, e nelle
difficoltà in cui incorse. Infatti già da questa semplice sinossi possiamo
enucleare i fondamenti teorici che sono alla base della moderna IA:
-
l’idea che il ragionamento, e in generale ogni tipo di attività
della mente, sia un calcolo
-
il concetto di simbolo o rappresentazione
-
il concetto di calcolo inteso come manipolazione di simboli in
base a regole
-
l’idea (implicita in
Hobbes) che possa esistere qualcosa come un
manipolatore automatico di simboli
Se ci pensate, alcuni dei
concetti che compaiono in queste proposizioni teoriche fanno parte del bagaglio
di concetti del senso comune: calcolo, rappresentazione o simbolo sono parole
che si usano abitualmente. Tuttavia in questo contesto essi assumono dei sensi
ben precisi, che non sono coincidenti con l’uso comune. Varrà dunque la pena
soffermarci su di essi per considerarli sotto una nuova luce.
Il concetto di
rappresentazione e di simbolo
Cominciamo con l’analisi
del concetto importantissimo di ‘rappresentazione’. Intuitivamente, tutti
siamo in grado di indicare esempi di rappresentazione:
-
un quadro è una rappresentazione
-
una foto è una rappresentazione
-
una cartina stradale è una
rappresentazione
Che cosa hanno in comune
questi esempi? Il fatto di essere delle cose che ci mostrano (in vario modo)
altre cose, persone o luoghi. Un ritratto, ad esempio, ci mostra l’aspetto di
una persona. Una cartina stradale, invece, ci mostra la disposizione delle
strade in una città o in una porzione di territorio. Generalizzando possiamo
dire che una rappresentazione è un oggetto che sta per, o raffigura un altro
oggetto. Una proprietà interessante delle rappresentazioni è che esse non
sono delle copie esatte dei loro oggetti. Tornando ai nostri esempi, un ritratto
rappresenta l’aspetto di una persona, ma non il suo tono di voce, la
morbidezza della pelle, o il profumo dei capelli, per non parlare del suo
carattere. Una rappresentazione dunque è sempre il prodotto di un processo di
selezione tra le molte (infinite) caratteristiche dell’oggetto da raffigurare,
ovvero di un processo di astrazione.
Le rappresentazioni si
dividono in due classi in base al rapporto che esiste tra oggetto rappresentante
e oggetto rappresentato. In alcuni casi, come per le foto, esiste una relazione
fisica che determina il modo in cui l’oggetto viene rappresentato. La luce
emessa dall’oggetto, ad esempio una casa, impressiona la pellicola
imprimendovi sopra l’immagine. In altri casi, come per il disegno siamo noi
che scegliamo come rappresentare la casa, usando delle linee verticali,
orizzontali o oblique. Tuttavia tanto il disegno quanto la fotografia mantengono
un rapporto di somiglianza o analogia con il loro oggetto. Questo tipo di
rappresentazioni sono appunto definite analogiche.
Ora, prendiamo il disegno
di una casetta, uno di quelli fatti dai bambini. Se analizziamo il disegno ci
accorgiamo che la sua forma può essere descritta come un quadrato a cui viene
sovrapposto un triangolo. Chiaramente abbiamo ancora a che fare con qualcosa che
assomiglia vagamente alla casa reale. Tuttavia arrivati a questo punto possiamo
fare un vero e proprio salto nel processo di astrazione. Infatti grazie alla
geometria analitica (inventata da Cartesio!) le figure geometriche sul piano
possono essere rappresentate mediante insiemi di equazioni. E quando
consideriamo queste equazioni, costruite utilizzando i simboli algebrici e
matematici, ci troviamo di fronte ad una rappresentazione della casa che
fisicamente non ha nulla a che fare con la casa stessa, ma che in qualche modo
continua a raffigurare alcune sue caratteristiche. Questo tipo di
rappresentazioni sono denominate analitiche.
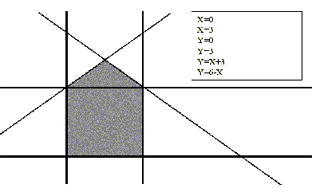
Figura 1 - La rappresentazione di una casa mediante equazioni
La rappresentazione della casa fatta mediante formule matematiche
ha alcune interessanti caratteristiche. In primo luogo essa si basa
su un insieme di segni ben definiti e distinti, cioè discreti (i
segni dell'algebra lineare): possiamo indicare questi segni con il
termine di simboli e possiamo dire che abbiamo una rappresentazione
simbolica della casa. In secondo luogo questi simboli non hanno
nulla a che fare con ciò che rappresentano: il fatto che siano
usati per rappresentare una certa figura geometrica, che assomiglia
a una casa, è frutto delle convenzioni e stipulazioni del sistema
algebrico che utilizziamo, ed è da questo punto di vista
arbitrario. Infine, ci accorgiamo facilmente che questi stessi
simboli possono essere usati per rappresentare altri oggetti: ad
esempio una scatola o un televisore. Basta che ci mettiamo d'accordo
prima su che cosa vogliamo rappresentare, e sul significato dei
simboli utilizzati.
Se ci pensiamo bene, anche le parole di una
lingua possono essere considerate rappresentazioni simboliche in
questo senso. Se prendiamo una parola, ad esempio "gatto",
ci accorgiamo che è composta da una sequenza di elementi distinti
chiaramente l'uno dall'altro: i singoli caratteri dell'alfabeto. (In
realtà il nostro esempio si riferisce alle parole scritte delle lingua. A
essere precisi dunque ci troviamo in presenza di un duplice livello di
rappresentazione: il primo è quello della scrittura che rappresenta la lingua
parlata, ed il secondo quello della lingua che rappresenta oggetti o situazioni
del mondo. Tuttavia i linguisti hanno dimostrato che anche il linguaggio parlato
è costituito da elementi di base discreti, i fonemi, e dunque l'argomento
varrebbe egualmente. Tenere conto di queste distinzioni, e delle molte
considerazioni e punti di vista che potrebbero suggerire formulazioni
alternative o più precise di quelle qui utilizzate, renderebbe tuttavia più
complicata l'esposizione; abbiamo quindi preferito… essere un po' generici.)
Possiamo dire che si tratta di un simbolo composto. Noi usiamo
questo simbolo per parlare e scrivere sui gatti e ci capiamo
perfettamente. Ma la parola "gatto", per quanto ci
mettiamo a guardare, non mostra alcuna somiglianza con alcun gatto
reale. Come i simboli matematici, anche i simboli della lingua
rappresentano ciò che rappresentano in virtù di una convenzione. Il
calcolo come manipolazione di simboli e i sistemi formali
Torniamo a considerare la rappresentazione di una casa per mezzo
di equazioni lineari. Molti di voi sapranno che grazie alle regole
dell'algebra possiamo usare queste equazioni per calcolare ad
esempio l'altezza della casa o la sua superficie. O meglio, per
calcolare l'altezza o la superficie delle figure geometriche che
rappresentano la casa. Ma che cosa facciamo quando effettuiamo
questi calcoli? Di norma scriviamo su un pezzo di carta delle
formule iniziali (le nostre equazioni), poi iniziamo a riscriverle
trasformando i simboli che le compongono in base a regole ben
precise. Che tipo di trasformazioni applichiamo? Spostiamo un
simbolo da una parte ad un'altra della formula; introduciamo nuovi
simboli o ne cancelliamo di esistenti. Tutto questo finché
arriviamo a scrivere una formula che costituisce il risultato dei
nostri calcoli. Quando si calcola dunque non si fa altro che
manipolare, nel senso che abbiamo visto, simboli (eventualmente
raccolti in formule) in base a regole esplicite. A ben vedere,
potremmo anche non sapere niente dell'algebra, della risoluzione
delle equazioni o dei sistemi di equazioni: basterebbe disporre di
un manuale che ci dicesse che tipo di trasformazioni possiamo
applicare in una determinata situazione, e saremmo in grado di
calcolare.
Questo modo di considerare il calcolo, che potrebbe
sembrare piuttosto limitativo, si dimostra invece una estensione
notevole della nozione di calcolo del senso comune. Essa infatti ci
consente di far rientrare nel dominio dei calcoli una serie di
fenomeni che normalmente non vengono considerati tali. Per capire
che cosa intendiamo con questa affermazione prendiamo, ad esempio,
un gioco banale come il tris. Come ognuno di voi saprà, nel tris
due giocatori scrivono a turno uno dei due simboli (di norma una
crocetta e un pallino) su una scacchiera composta da nove caselle.
Per ogni turno di gioco ciascun giocatore può scrivere il suo
simbolo in una qualunque delle caselle, purché sia libera. Lo scopo
del gioco è allineare tre simboli eguali sulla scacchiera in
verticale, orizzontale o diagonale; in alternativa il gioco finisce
quando tutte le caselle sono state riempite. Se analizziamo questo
gioco ci accorgiamo che abbiamo:
-
due simboli che si distinguono
per la loro forma
-
una posizione iniziale del gioco: nel nostro
caso, la scacchiera vuota
-
una regola precisa che ci dice per ogni
singolo turno del gioco quali sono le mosse consentite;la regola è
semplicissima: è possibile scrivere il proprio simbolo su ogni
casella che non sia occupata
-
un insieme di posizioni finali che
dicono quand'è che una partita finisce, e chi ha vinto
Giocare un
gioco come il tris, dunque, corrisponde ad effettuare un processo di
calcolo nel senso che abbiamo visto sopra. Per verificarlo proviamo
a trasformare il gioco del tris in questo modo: rappresentiamo le
caselle della scacchiera usando le nove cifre della numerazione
decimale; la prima casella in alto a sinistra diventa '1', la
seconda '2' e così via. Per i caratteri che vanno scritti nella
scacchiera potremo usare i simboli 'X' e 'Y'. Infine, per indicare
in quale casella è stato inserito un carattere scriveremo prima il
simbolo del carattere poi la cifra della casella, in questo modo:
'X1' significa che la X è stata scritta nella prima casella in
altro a sinistra.
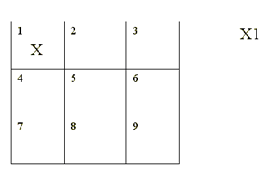
Figura 2 - La traduzione del tris in un sistema formale
Il gioco consiste nello scrivere per passi
successivi una sequenza di coppie simbolo/cifra con il vincolo che
ogni cifra può essere usata solo un volta, e in due coppie
adiacenti simbolo/cifra non deve comparire due volte lo stesso
simbolo (quest'ultima condizione corrisponde al fatto che i due
giocatori devono alternarsi nell'effettuare le loro 'mosse'). La
partita finisce quando si verifica una di queste due condizioni:
-
nella sequenza di coppie uno dei due simboli di carattere compare,
in qualsiasi ordine, insieme alle cifre delle seguenti terne: (1 - 2
- 3), (4 - 5 - 6), (7 - 8 - 9), (1 - 4 - 7), (2 - 5 - 8), (3 - 6 -
9), (1 - 5 - 9), (3 - 5 - 7);
-
la sequenza è costituita da nove coppie
Cominciamo a giocare. Al primo passo scriviamo X1. Al
secondo passo introduciamo Y9, ottenendo X1Y9. Al terzo passo
introduciamo X5, ottenendo X1Y9X5. Andando avanti per sei passi
possiamo trovare questa sequenza: X1Y9X5Y8X6Y7. Bene, il gioco è
finito: infatti il simbolo Y in questa sequenza si trova associato
ai numeri di una delle terne che avevamo elencato sopra. Se volete
potete trasformare questa sequenza nella corrispondente situazione
della scacchiera: verificherete che ci saranno tre Y in sequenza
nell'ultima riga!
L'esempio che abbiamo fatto è piuttosto banale,
ma ci permette di capire in che senso la nozione di calcolo, intesa
come manipolazione di simboli in base a regole è una nozione molto
vasta. Essa infatti descrive il funzionamento di tutti quei sistemi
che operano in base ad un insieme (finito) di elementi di base
formalmente distinti e ad un insieme (finito) di regole che
specificano le possibili trasformazioni di quei simboli. I sistemi
di questo tipo sono denominati sistemi formali. Un'altra conseguenza
che possiamo trarre dal nostro esempio è che i sistemi formali (tra
cui il tris) per funzionare non dipendono da nessuna caratteristica
del mezzo con cui sono costruiti. Per giocare a tris non ha alcuna
importanza di che materiale siano fatti la scacchiera e i simboli:
possiamo disegnare la scacchiera su un foglio di carta; possiamo
immaginare di costruire il tutto in legno come una piccola dama
cinese; o possiamo trasformare il gioco come abbiamo visto, nella
scrittura di una sequenza di formule.
La classe dei sistemi formali
è molto vasta. Giochi come la dama, gli scacchi, i giochi di carte,
sono sistemi formali. Ma anche l'aritmetica e la logica sono sistemi
formali. Secondo i teorici dell'intelligenza artificiale, infine,
anche il pensiero può essere descritto come un sistema formale. La
macchina di Turing e la teoria rappresentazionale della mente
Se osserviamo il sistema formale che abbiamo
costruito nel paragrafo precedente, notiamo che il suo funzionamento
è completamente determinato dalla forma dei simboli e dalle regole
di manipolazione. Non bisogna sapere nient'altro per farlo
funzionare; soprattutto, non è richiesto nessun intervento creativo
o intelligente. Questo vale per tutti i sistemi formali, per quanto
complessi e articolati essi possano essere. Ma allora, nulla ci
vieta di costruire una macchina che sia in grado di funzionare come
un sistema formale.
Naturalmente questa macchina deve essere una
macchina particolare: un'automobile, ad esempio, non farebbe al caso
nostro. Le caratteristiche di una macchina in grado di eseguire
questo genere di compiti sono state definite in modo rigoroso dal
logico e matematico Alan Turing in saggio pubblicato nel 1936 dal
titolo Sui numeri computabili con una applicazione al "problema
della decisione". L'obiettivo di Turing quando scrisse questo
saggio era quello di risolvere alcuni complicati problemi logici che
erano di grande interesse a quei tempi.
Ma l'interesse di questo
breve scritto non consiste solo in questo. Ciò che veramente è
interessante è il metodo utilizzato da Turing. In tale metodo,
infatti, troviamo per la prima volta molte delle idee alla base
della moderna scienza dei calcolatori da un lato e della
intelligenza artificiale dall'altro. Nel suo saggio infatti, Turing
immagina una specie di macchina teorica, molto semplice, che facendo
delle banali operazioni doveva essere in grado compiere qualunque
tipo di calcolo, di qualsiasi genere. Oggi questa macchina viene
comunemente denominata macchina di Turing.
Una macchina di Turing è
costituita da un dispositivo, una specie di testina, che può
scrivere e leggere simboli, ad esempio 0 e 1, su un nastro. Il
nastro è diviso in celle, ognuna della quali contiene un solo
simbolo, e può avere una lunghezza potenzialmente infinita. La
testina, oltre a scrivere, può spostarsi a destra o a sinistra, una
cella alla volta. Inoltre può assumere un certo numero di stati
interni distinti. 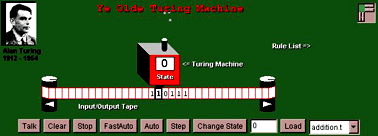
Figura 3 - La macchina di Turing simulata da un applet Java
(disponibile all'indirizzo
http://www.bvu.edu/faculty/schweller/tmachine.html)
Il
funzionamento della macchina avviene per passi successivi. Il suo comportamento
ad ogni passo è determinato da regole, che tengono conto del simbolo che la
testina legge sul nastro e del suo stato interno. Ad esempio: se la testina
legge il simbolo 0 e si trova nello stato A, la regola potrà dirle di scrivere
1 al posto dello '0' e di spostarsi a destra, passando allo stato B.
Specificando opportunamente una serie di regole come questa, la macchina di
Turing è in grado di calcolare moltissime cose. Di più: è in grado di
svolgere tutti i calcoli che sappiamo eseguire con altri metodi. Ma non basta.
Non c'è alcuna ragione per cui i simboli di una Macchina di Turing debbano
rappresentare numeri. Anzi, come sappiamo, di per sé un simbolo può
rappresentare qualsiasi cosa. E se esistono delle regole che ci dicono come
manipolare tali simboli in modo sensato, ebbene, una macchina di Turing può
farlo. In effetti si può dimostrare che una macchina di
Turing, dotata delle
opportune istruzioni, è in grado di simulare il funzionamento di qualsiasi
sistema formale. Anzi, la classe dei sistemi formali corrisponde esattamente
alla classe delle funzioni che una macchina di Turing può calcolare. Potremmo
anche dire che una macchina di Turing è una specie di sistema formale
automatico. Inoltre, sappiamo anche che tutti i moderni calcolatori digitali
sono equivalenti a una macchina di Turing, nel senso che un computer può fare
tutto quello che una macchina di Turing può fare. Di conseguenza possiamo dire
che un computer digitale è in grado di far funzionare (o di funzionare come)
qualsiasi sistema formale. Non ci possiamo soffermare ulteriormente su queste
considerazioni, poiché si tratta di argomenti di notevole complessità che
richiederebbero una competenza specialistica. Ma quanto abbiamo detto ci è
sufficiente per tornare al nostro discorso sui fondamenti dell'intelligenza
artificiale. Infatti, se ipotizziamo che i processi che avvengono nella nostra
testa quando pensiamo, ragioniamo, parliamo e capiamo possono essere descritti
come sistemi formali, potremmo concludere che anche il cervello è una specie di
macchina equivalente a una macchina di Turing e inter alia a un computer
digitale. Questo non vuol dire che nel nostro cervello ci deve essere una
testina che scrive simboli su un nastro infinito, o una CPU. Stiamo soltanto
dicendo che - se partiamo da questa prospettiva - le operazioni che avvengono
nel nostro cervello quando pensiamo sono manipolazioni di simboli, fisicamente
rappresentati, secondo regole; detto in altri termini, sono una specie di
programmi. (I simboli mentali, naturalmente, sarebbero diversi da quelli usati
dai computer, ma per quel che concerne la loro utilizzazione nell'ambito dei
processi di calcolo ciò che conta è solo la loro forma. Abbiamo visto infatti
che il mezzo con cui viene costruito un sistema formale non ha alcuna influenza
sul suo funzionamento.) Questa teoria sulla natura del pensiero viene
comunemente indicata come teoria rappresentazionale della mente, e costituisce
uno dei fondamenti teorici di molta parte dell'intelligenza artificiale.
Infatti, se la suddetta teoria è vera, il problema di riprodurre su un computer
digitale le capacità cognitive degli esseri umani si 'ridurrebbe' a quello di
trovare le regole con cui il nostro cervello elabora i simboli mentali, e
trasformarle in programmi.
|